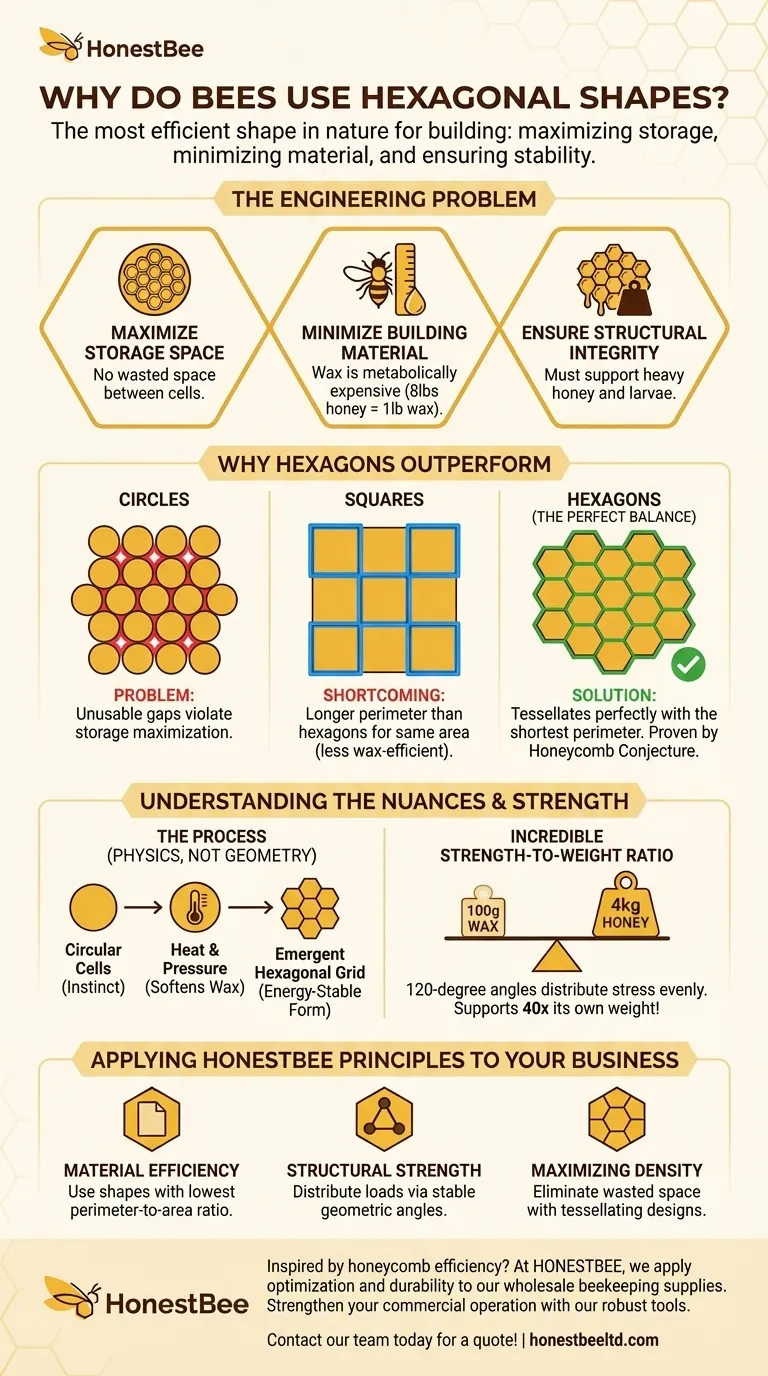
蜜蜂使用六边形只有一个简单的原因:它是自然界中最有效的建造形状。 六边形网格在构建细胞格时,使用的材料——即蜂蜡——最少,同时能提供最大的存储空间和结构完整性。这是一个经过数百万年进化打磨的完美解决方案。
蜂巢中的六边形并非随意选择;它是对一个复杂工程问题的数学最优解。它代表了在最小化建筑材料、最大化存储容量和确保结构稳定性之间的完美权衡。
蜜蜂必须解决的工程问题
要理解六边形的巧妙之处,我们必须首先了解蜜蜂面临的挑战。它们需要一个能满足三个关键工程要求的结构。
最大化存储空间
蜂群的生存取决于存储尽可能多的蜂蜜和花粉。因此,存储单元的形状必须是空间效率最高的,彼此之间不能留下任何浪费的空隙。
最小化建筑材料
蜜蜂大约需要消耗八磅蜂蜜才能生产一磅蜂蜡。这使得蜂蜡成为一种代谢成本高昂的资源,不能浪费在低效的设计上。理想的形状必须用最短的周长围出给定的面积。
确保结构完整性
一个建成的蜂巢非常重。该结构必须足够坚固,不仅能支撑蜂蜜的重量,还能支撑正在发育的幼虫,而且这一切都是用相对脆弱的材料构建的。

为什么六边形优于其他形状
当根据这些需求进行评估时,六边形是唯一能完美满足所有条件的形状。其他常见的形状,如圆形和正方形,都有明显的缺陷。
圆形的弊端
从技术上讲,圆形是以最短的周长容纳最大面积最高效的形状。然而,当圆形紧密排列在一起时,它们会留下无法使用的空隙,这违反了最大化存储空间的需求。
正方形的不足
正方形、三角形和六边形是唯一可以密铺(tessellate)的规则多边形,这意味着它们可以在平面上紧密排列而没有空隙。虽然正方形解决了空隙问题,但要围出相同面积,正方形比六边形需要更长的周长,因此在蜂蜡使用效率上不如六边形。
六边形的完美平衡
六边形是更优的选择,因为它既能完美密铺,又拥有所有可以密铺的形状中最短的周长。这一原理非常基本,它在1999年的“蜂巢猜想”(Honeycomb Conjecture)中得到了数学证明。它是理想的中间地带,以最低的材料成本提供最大的存储空间。
理解权衡和细微差别
尽管我们赞叹蜂巢完美的几何形状,但这个过程更多的是蜜蜂利用物理学,而不是它们是设计大师。
这不是有意识的几何学
蜜蜂不会有意识地测量角度。这种六边形结构是由本能和物理力驱动的涌现属性(emergent property)。蜜蜂将大致圆形的单元靠得很近建造。
热量和压力的作用
蜜蜂身体产生的热量使蜡软化。周围单元的表面张力和压力随后将圆形结构拉伸成最节能、最紧凑的形式——一个完美的六边形网格。
惊人的强度重量比
最终的结构是高效设计的证明。单元壁相交处的120度角非常适合均匀分散应力。这使得一个仅重100克的蜂巢能够支撑高达4公斤的重量,这是自然工程学中的一项惊人壮举。
如何将此应用于您的项目
蜂巢设计背后的原理不仅限于蜜蜂。它们为工程、设计和物流提供了有力的借鉴。
- 如果您的首要重点是材料效率: 使用具有最低周长/面积比且可以平铺的形状,六边形是理想的选择。
- 如果您的首要重点是结构强度: 像蜂巢一样,通过共享墙壁和稳定的几何角度来分配载荷。
- 如果您的首要重点是最大化密度: 确保您的设计使用可以密铺的形状,消除单元之间任何浪费的空间。
蜂巢是优化方面的典范,展示了简单的物理原理如何能产生极其坚固和高效的结构。
摘要表:
| 要求 | 六边形为何表现出色 |
|---|---|
| 最大化存储 | 完美密铺,单元之间零空间浪费。 |
| 最小化材料(蜡) | 在所有可密铺的形状中,具有最短的周长/面积比。 |
| 确保结构完整性 | 120度的交角均匀分散应力,带来惊人的强度。 |
受到蜂巢效率的启发? 在 HONESTBEE,我们将优化和耐用性的相同原则应用于我们的养蜂用品。我们为商业蜂场和养蜂设备经销商提供所需的高强度、高质量工具,以建立强大且富有成效的业务。让我们讨论一下我们以批发为重点的解决方案如何能加强您的业务。立即联系我们的团队获取报价!
图解指南